Beispiel: A = {n
Lösung der Hausaufgabe
Def. Menge: Eine Menge ist eine Zusammenfassung bestimmter, wohl unterschiedlicher Dinge unserer Anschauung oder unseres Denkens, welche Elemente der Menge genannt werden, zu einem Ganzen.
Beschreibung von Mengen:
Alle enthaltenen Elemente werden aufgezählt.
Beispiel: A = {2,4,6,8}
Eine Eigenschaft wird angegeben, die die Elemente erfüllen müssen, um zur Menge zu gehören.
Beispiel: A = {n ![]()
![]() | n gerade}
| n gerade}
Es wird unendlich aufgezählt.
Beispiel: A = {2,4,8, ...}
Def. Teilmenge
Eine Menge A heißt Teilmenge einer Menge B, wenn jedes Element von A auch Element von B ist. Schreibweise: A![]() B
B
Def. Leere Menge
Eine Menge heißt Leere Menge, wenn die Menge keine Elemente enthält. Schreibweise: ![]() oder {}
oder {}
Bezeichnungen
| andere Schreibweise | ||
| x |
x ist Element der Menge A. | |
| x |
x ist nicht Element der Menge A. | |
| A |
A ist Teilmenge von B | x |
| A |
A ist echte Teilmenge von B | A |
| A = B | Mengengleichheit | x |
| { |
Menge von leerer Menge als Element | |
| |A| | Kardinalität - Anzahl der Elemente einer endlichen Menge |
Definition
A |
Vereinigungsmenge von A und B | 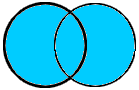 |
A |
Schnittmenge von A und B | 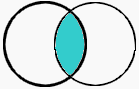 |
A \ B |
Differenzmenge A - B | 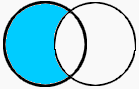 |
| _ |
Komplement (Negation der Aussage) von A | |
|
symmetrische Differenz von A und B | |
| Potenzmenge von A (Menge. deren Elemente selbst Mengen sind) |
| Gesetze | Venn-Diagramme |
||
| Kommutativgesetze |  |
A |
|
| Assoziativgesetze |  |
(A (A |
|
| Distributivgesetze | 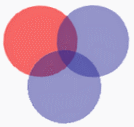 |
 |
A A |
| Gesetze für das Komplement |  |
A |
|
| Gesetze von DeMorgan |  |
_____ _ _ A _____ _ _ A |
|
| Idempotenzgesetze | A |
||
In der folgenden Tabellewerden Mengenalgebra und Aussagenalgebra gegenübergestellt:
| Boolesche Algebra | Mengenalgebra | Aussagenalgebra | Schaltalgebra | ||
| V | Potenzmenge | {0,1} | Wahrheitswerte | ||
| * | Durchschnitt |
Schnittmenge | Konjunktion |
Konjunktion | |
| + | Vereinigung |
Vereinigungsmenge | Disjunkion |
Disjunktion | |
| -1 | Komplement ¯¯ | Komplementärmenge | Negation |
Negation | |
| e | T | Trägermenge | 1 | Wahr (True) | |
| n | Leere Menge | Kontradiktion | 0 | Falsch (False) | |
| Teilmengenrelation A |
ImplikationsaussageA |
||||
| Gleichheitsrelation A = B | Äquivalenzaussage A |
| a) AB |