Der gerichtete Graph

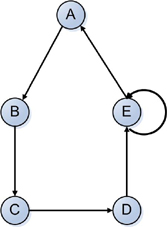
Ein gerichteter Graph enthält gerichtete Kanten, für die jeweils ein Start- sowie ein Endknoten definiert ist. Enthält ein Graph keine gerichteten Kanten, nennt man ihn ungerichtet.

G - Graph, Menge von Knoten und Kanten. G = (V,E)
E - Kantenmenge
V - Knotenmenge

- Jede Kante hat einen Anfangs- und einen Endknoten.
- Ein Kreis ist ein zum Ausgangsknoten zurück führender Weg. (siehe Knoten E)
- Ist (u, v) Kante eines gerichteten Graphen, so ist (u,v) inzident von Knoten u und inzident von Knoten v.
- Außerdem sagt man, dass der Knoten v adjazent (benachbert) u Knoten u ist.
- Grad eines Knotens - Zahl der Kanten,die im Knoten enden
- Endlich ist ein Graph, wenn die Menge der Knoten und die Menge der Kanten endlich sind
- Adjazenzmatrix - Der Graph wird in Tabellenform gespeichert.
- Adjazenzlisten - Hier wird für jeden Knoten eine Liste seiner Nachbarn gespeichert.

Aufgabe a) Erstellen Sie zu diesem Graphen die Adjazenzmatrix sowie die Adjazenzlisten!
	A: {      } B: {      } C: {      } D: {      } E: {      }	A B C D E A           B           C       1   D           E
Aufgabe b) Ajazenzmatrix: Zeichnen Sie den entsprechenden Graphen!
A B C D E F A 0 1 0 0 0 1 B 0 0 1 0 0 0 C 0 1 0 1 0 0 D 0 0 1 0 0 0 E 0 0 0 1 0 0 F 0 0 0 0 1 0

Vorlesung zu Graphen und Algorithmen (Video) , Teil 1
Vorlesung zu Graphen und Algorithmen (Video) , Teil 2
Das Knotenübedeckungsproblem

Der ungerichtete Graph

Die Kantenmenge besteht aus ungeordneten Paaren, Schleifen sind nicht erlaubt.

Ist (u, v) Kante eines ungerichteten Graphen, so ist (u,v) inzident mit u und v.

Der vollständige Graph

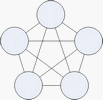
Zwischen jedem Knotenpaar existiert eine Kante. Also hat ein vollständiger Graph mit n Knoten Kanten.