Abstrakter Datentyp Schlange |
zurück zu den anderen ADT Hefteintrag  |
Synonyme: FIFO-Schlange, Warteschlange, Queue
Der DT Schlange kann als spezielle Liste aufgefasst werden, bei der die Elemente an einem Ende (hinten) eingefügt und am anderen Ende (vorne) entfernt werden.
Def.: Eine Schlange ist eine (ggf. leere) Folge von Elementen zusammen mit einem so genannten (ggf. undefinierten) Front-Element.
|
Operationen |
|
vor der OP |
nach der OP |
|
CREATE |
erzeugt leere Schlange |
|
|
|
INIT(S) |
initialisiert S als leere Schlange |
|
Die Schlange ist zur weiteren Bearbeitung vorbereitet, sie ist leer, da sie keine Elemente enthält. |
|
ENQUEUE (S, x) |
fügt Element x am Ende der Schlange S ein |
Die Schlange ist nicht leer. |
Als letztes wurde x in der Schlange abgelegt. |
|
DEQUEUE (S) |
löscht Element, das am längsten in der Schlange S verweilt (erstes Element) |
Die Schlange ist nicht leer. |
Das erste Element wurde entfernt. |
|
FRONT(S) |
fragt erstes Element in der Schlange S ab |
Die Schlange ist nicht leer. |
Die Schlange ist nicht verändert. |
|
EMPTY(S) |
fragt ab, ob die Schlange S leer ist |
Die Schlange ist vorhanden und zumindest initialisiert. |
Falls die Schlange keine Elemente enthält, wird true geliefert, ansonsten false. |
- Druckerwarteschlange (Puffer für Druckaufträge) - zeitliche Entkoppelung
- Aufbau einer Internet-Seite - Browser holt die IP-Paket aus einem internen Puffer ab und baut die Seite auf.
- Algorithmen auf Bäumen oder auf Graphen - Breitensuche
- Pufferung von Daten vor ihrer Weiterverarbeitung
- Pufferung von Maus- und Tastaturereignissen (auf graphischen Oberflächen), um sie dann den korrekten Prozessen zuzuweisen
- Parallelisieren - wie bei einem Postamt mit mehreren Schaltern, an denen parallel die in einer Schlange wartendne Kunden bedient werden
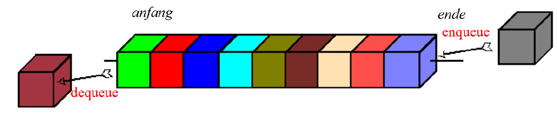
Das erste Element, das Front-Element (lila),
muss direkt ersichtlich sein. Der Kopfzeiger anfang zeigt
darauf.
Jedes Element muss auf seinen Nachfolger zeigen. Hier wird dies durch den Pfeil
angedeutet, z. Bsp. (grün) -> (rot
).
Und das letzte Element (blau) muss als das letzte
erkennbar sein. Der Fuß-Zeiger ende zeigt darauf.
Beim ADT Schlange handelt es sich um eine Listenstruktur zur Verwaltung
eines allgemeinen, einheitlichen Datentyps nach dem FIFO-Prinzip, d.h. die
Werte werden in der gleichen Reihenfolge entnommen, in der sie eingetragen
wurden.
Anders gesagt: Man kann nur auf das Element zugreifen, das am längsten im
Behälter ist. An den Schwanz der Schlange werden mit der Operation enqueue
Datenelemente angehängt. Am Kopf kann das erste Element first(S) mit der
Operation dequeue abgeholt werden.
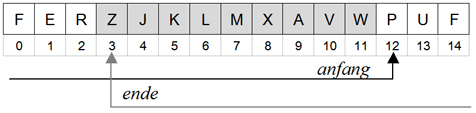
Implementierung mittels Array
Die Größe des Arrays bestimmt die Puffergröße. Die
Begrenzungen des Puffers werden durch zwei Zeiger markiert.
Problematisch bei dieser Implementierung ist, dass die Zeiger anfang und ende immer nur erhöht werden. Deshalb:
Implementierung mittels „zirkulärem“ Array
Das erste Element folgt wieder auf das letzte. Dies nennt
man auch zyklische Liste. Man stelle sich vor, dass rechter und linker Rand des
Arrays miteinander verbunden sind.
|
1. Frage: Wenn anfang = ende
- ist der Puffer voll oder leer? |
|
2. Probieren Sie das Programm |
